09 Gradients

09 Gradients#

Multivariable Calculus is a branch of calculus that extends the concepts of single-variable calculus (like derivatives and integrals) to functions of multiple variables. It’s used to study phenomena in higher dimensions, such as physical phenomena that depend on multiple variables.

Let:

\[f: \mathbb {R}^ d \to \mathbb {R}\]
\[\begin{split}\displaystyle \theta =\begin{pmatrix} \theta _1\\ \theta _2\\ \vdots \\ \theta _ d\end{pmatrix} \mapsto f(\theta )\end{split}\]

The gradient of \(f\) is the vector-valued function

\[\displaystyle \displaystyle {\color{blue}{\nabla _\theta }} f: \mathbb {R}^ d \to \mathbb {R}^ d\]
\[\begin{split} \nabla _\theta f(\theta )=\quad \displaystyle \left.\begin{pmatrix} \frac{\partial f }{\partial \theta _1}\\ \frac{\partial f }{\partial \theta _2}\\ \vdots \\ \frac{\partial f }{\partial \theta _ d}\end{pmatrix}\right|_{\theta }. \end{split}\]

In multivariable calculus, the gradient of a function measures how much the function changes if you move a tiny bit in each possible direction. It’s a vector that points in the direction of the greatest rate of increase of the function, and its length gives the rate of increase in that direction.

Let’s consider a simple function of two variables, f(x, y) = x^2 + y^2. This function represents a bowl-shaped surface in three dimensions.

The gradient of this function is a vector that points in the direction of the steepest uphill slope from any point on this surface. It’s given by the vector of partial derivatives of the function with respect to each variable

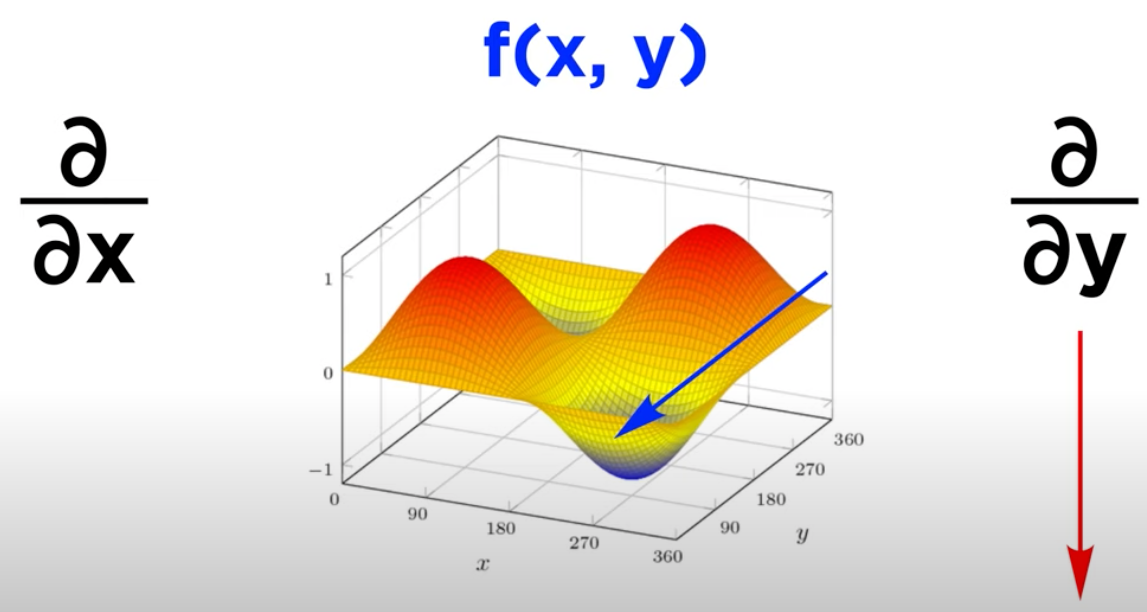
  • Partial derivative of f with respect to x: ∂f/∂x

  • Partial derivative of f with respect to y: ∂f/∂y $\(∇f = [∂f/∂x, ∂f/∂y]\)$

What is partial derivative of function f(x)#

Lets recap For a function \(f(x)\), the derivative \(f'(x)\) can be found by applying the rules of differentiation. Here are some basic rules:

  1. Constant Rule: The derivative of a constant is 0.

  2. Power Rule: The derivative of \(x^n\) is \(n*x^{n-1}\).

  3. Product Rule: The derivative of \(u*v\) is \(u'*v + u*v'\).

  4. Quotient Rule: The derivative of \(u/v` is `(u'*v - u*v') / v^2\).

  5. Chain Rule: The derivative of \(f(g(x)) ` is ` f'(g(x)) * g'(x)\).

Where u and v are functions of x, and u' and v' are their respective derivatives.

youtube video on Partial Derivatives

image.png

\(f'(x) == df/dx\). Its just different way to express differentiation image-2.png

it can also be represented with partial symbol \(\partial\) instead of \(d\) i.e. \(\frac{\partial }{\partial x }\) is partial derivative with respect to x (move in direction of x) where y is constant. Similarly \(\frac{\partial }{\partial y }\) is partial derivative with respect to y (move in direction of y) where x is constant

image-3.png

In Python, you can use the sympy.diff function to compute derivatives. For example:

import sympy as sp

x, y = sp.symbols('x y')
f = x*y**2 + x**3

# Partial derivative of f with respect to x
f_x = sp.diff(f, x)
# Partial derivative of f with respect to y
f_y = sp.diff(f, y)
print(f"∂f/∂x: {f_x}")
print(f"∂f/∂y: {f_y}")

∂f/∂x: 3*x**2 + y**2
∂f/∂y: 2*x*y

Let’s consider a simple function of two variables, $\(f(x, y) = x^2 + y^2\)$

This function represents a paraboloid in three dimensions.

The gradient of this function is a vector that points in the direction of the greatest rate of increase of the function. It’s given by the vector of partial derivatives of the function with respect to each variable:

\[∇f = [∂f/∂x, ∂f/∂y] = [2x, 2y]\]

Let’s compute the gradient of f in the form of vector using Python:

import numpy as np
from scipy.optimize import minimize

import sympy as sp

theta_1, theta_2 = sp.symbols('theta_1 theta_2')
f = theta_1**2 + theta_2**2

# Partial derivative ∂f/∂theta_1 with respect to theta_1
f_theta_1 = sp.diff(f, theta_1)
# Partial derivative ∂f/∂theta_2 with respect to theta_2
f_theta_2 = sp.diff(f, theta_2)

# Evaluate the gradient f(theta)
print(f"[∂f/∂theta_1, ∂f/∂theta_2] = [{f_theta_1}, {f_theta_2}]")

[∂f/∂theta_1, ∂f/∂theta_2] = [2*theta_1, 2*theta_2]
Contents